 |
Handledning till programmet "SPEKTRAL" |
OBS! FÖR UTSKRIFT KAN DET VARA LÄMPLIGT ATT LADDA NER HANDLEDNINGEN SOM WORD-DOKUMENT (1 Mb)
 |
Handledning till programmet "SPEKTRAL" |
UPPSTARTNING
Programmet består av en exe-fil samt ett antal datafiler (de senare i ASCI-kod). Kopiera över det hela till en lämplig mapp på hårddisken. Starta genom att klicka på den fil som heter "spekt.exe" . Du får upp en meny där endera av fem alternativ kan väljas, med hjälp av en liten grön pil, som manövreras med piltangenterna upp/ner. När den pekar på önskat alternativ, tryck <Enter>.
Programmet använder SVGA i upplösningen 800 x 600 med 256 färgers palett. Det går bra att köra under Windows 95 och 98 och självfallet under MS-DOS. På vissa datorer med Windows NT4 kan hårdvaran vara svår att nå fram till. I så fall kan man dock vanligtvis köra programmet direkt från disketten. Starta i så fall om datorn med systemdiskett för DOS eller Windows95/98. Sätt därefter (dvs när prompten A:\> kommit upp) in programdisketten, skriv spekt och tryck <Enter>.
DE FEM TABLÅERNA
TABLÅ 1 : Spektralfördelning och färg
Detta är den grundläggande tablån, som visar sambandet mellan spektral energi-fördelning hos ett ljusflöde och den färg detta ljus synes ha. Den ser ut så här, efter tryck på tangent 5, som ett exempel:
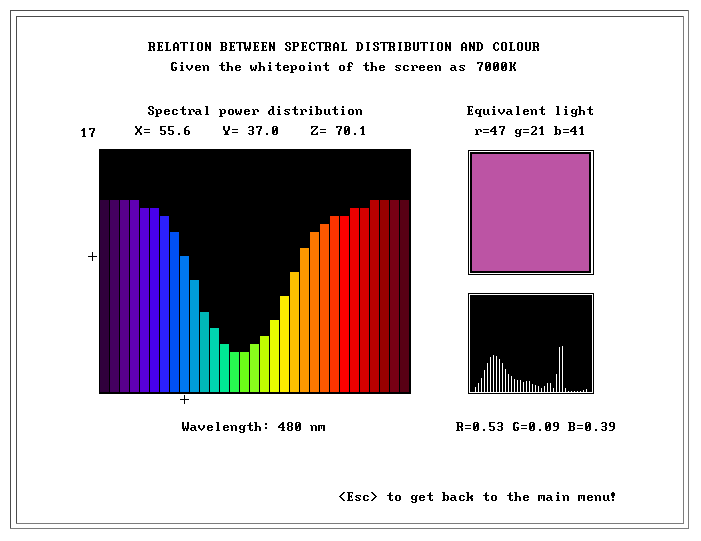
I den stora rutan visas spektralfördelningen, i den lilla rutan visas den motsvarande färgen. Genom att trycka på en av siffertangenterna 1 - 8 beställer du fram ett antal färdiga exempel. Du kan ta något av dem till utgångspunkt och sedan, med piltangenternas hjälp, modifiera spektralfördelningen. Den återges med 31 samplingspunkter, från 400 nm t.o.m. 700 nm. Varje punkt motsvarar således ett intervall på 10 nm. I varje intervall kan 30 intensitetsnivåer väljas. (Det ger m.a.o. 3130 möjliga spektralfördelningar!) I exemplet i figuren är fördelningens nivå som synes 17 vid 480 nm.
Du kommer att märka, att det för vissa spektralfördelningar, du tillverkar, inte går att visa motsvarande färg på bildskärmen. Det skulle nämligen i de fallen vara en färg med större mättnad (kulörstyrka) än vad som går att få fram med hjälp av ljuset från fosforerna RGB. I sådana fall visas bara svart. (Mer om detta nedan!)
Får du fram en intressant fördelning, som du vill spara, tryck då tangent S , så sparas färgen som en fil med namnet "spekt1.dat". Denna fil kan du senare beställa fram igen, genom att trycka tangent 0.
De färdiga exemplen är följande:
Du kan experimentera med Nr 1, genom att sänka staplarna på den kortvågiga (blå) sidan och se hur färgen blir mer mättat gul. På samma sätt kan du med Nr 2 få en starkare blå färg genom att dra ner staplarna på den långvågiga sidan. Med Nr. 3 kan du pröva med att dra upp stapeln vid en eller annan våglängd och se hur pass mycket avvikelse från konstant fördelning som behövs för att man skall se en kulörton hos färgen. Med Nr. 6 och 7 kan du pröva hur långt du kan intensifiera färgen (gulheten resp blåheten) innan skärmen ger upp, dvs inte klarar att återge större kulörthet.
Dock - intressantare experiment kan göras i de följande tablåerna. Tablå 1 ger emellertid anledning till några viktiga frågor. Se nedan!
TABLÅ 2: Ekvivalenta spektralfördelningar
Här visas två spektralfördelningar. Var och en av dem kan väljas fritt, genom tryck på någon av siffertangenterna 1 - 8. Därefter kan du modifiera den, efter önskan, med hjälp av piltangenterna.
Du växlar mellan de två fördelningarna genom tryck på mellanslagstangenten.
De två intilliggande fälten, i rutan ovanför, visar de två motsvarande färgerna. Du kan alltså justera de två fördelningarna så att de ger exakt samma färg, vilket kallas att de är metamera.
Följande färdiga fördelningar kan beställas fram med tangent 1-8:
Vänstra rutan: halmgult, ljublått, grått, grönt, blått, grått, D65, variabel nivå
Högra rutan: gult, blått, grått, magenta, blått, grått, trebandsljus, variabel nivå
Om du t.ex. till vänster beställer fram nr 3, så kan du till höger prova dig fram till vilken av de givna fördelningarna som ger exakt samma färg. I detta fall får du två metamera grå. Fortsätt med att undersöka vilka övriga kombinationer som är metamera!
Tablå 2 används för att tillverka ett par av fördelningar som man vill studera vidare i tablå 3,4 eller 5.
Upprepade tryck på 8 ger dig möjlighet att utgå från konstant fördelning på valfri nivå.
Genom tryck på X kan du omväxlande visa fördelningarna i samma skala - och därmed färgerna i korrekt ljushetsförhållande) eller var och en för sig optimerad till maximal luminans på skärmen.
Genom ett tryck på tangenten S kan du spara de två för tillfället uppsatta fördelningarna, för att använda dem i tablå 3,4 eller 5, eller för att ta över dem i ett matematikprogram etc. Genom ett tryck på tangent 0 kan du åter ta fram det par av spektralfördelningar du tidigare sparat, t.ex. för att vidare modifiera dem. De heter "spek2v.dat" respektive "spek2h.dat".
Genom tryck på 9 kan du ta fram det par av spektralfördelningar du sparat från tablå 3.
TABLÅ 3: Metameri och komplementaritet
Här visas återigen två spektralfördelningar och motsvarande färger sida vid sida, men i detta fall är de kopplade, på så sätt att det man tar bort från den ena adderas till den andra. Tangenterna 1 - 4 ger, som förut, några givna alternativ att utgå från. Tangent 0 och 9 möjlighet att ta fram tidigare sparat par, respektive ett par du sparat från tablå 2.
De givna exemplen är följande:
1. Till vänster gult, till höger svart. Från den vänstra kan du nu ta bort våglängderna i det gula området av spektrum, (dvs 570 nm och 580 nm) som då i stället kommer upp i den högra fördelningen. Den högra rutan får en mörkt brun ton. Det är emellertid ett ljus som är helt ekvivalent med det till vänster, så när som på att luminansnivån är så mycket lägre. Om du trycker på tangent X anpassas ljusnivån i vardera rutan så att maximal luminans på bildskärmen utnyttjas. Då blir de båda lika. Du har alltså, sida vid sida, två likadana gula ljus, det ena (till höger) helt dominerat av ljus med våglängd som motsvarar det gula området i spektrum. (Den svaga bakgrunden av ljus vid andra våglängder måste finnas med för att ljuset skall gå att återge på bildskärmen.) Det andra ljuset (till vänster) kännetecknas av att det innehåller alla våglängder utom just i det gula området, dvs 570 och 580 nm. Detta visar att det inte är vilken våglängd som dominerar i en spektralfördelning som avgör färgen, utan fördelningens utseende som helhet. Det avgörande, för att ett ljus skall motsvara gult, är att det har relativt lite energi vid korta våglängder, dvs i den violetta delen av spektrum.
2. Till vänster gulorange, till höger mörkt grått. Här har du på liknande sätt två ljus som kan göras färgmässigt lika. Från den vänstra tar du bort våglängderna kring det gula området av spektrum, (dvs först 580 nm, därefter 570 och 590 nm, så delar av 560 och 590 nm) vilka då i stället växer upp i den högra fördelningen. Den högra rutan blir samtidigt alltmer lik den vänstra. Du kan komma fram till två exakt lika gulbruna färger. De två fördelningarna är då metamera. De har samma gula färg, men den ena domineras av ljus i det gula området av spektrum; den andra har just inget ljus alls i det gula området av spektrum. Trycker du nu på X så får du se dem i ett ljusare läge. De är fortfarande identiska, men nu mera rent gyllengula. Trycker du 2 ser du att de dessutom är lika den ursprungliga fördelningen.
Anmärkning: Att man i 1 och 2 redan från början har lite neutral fördelning i högra rutan beror på att datorskärmen inte är kapabel att återge fullt mättade färger.
3. Nu går vi över till komplementfärger i förhållande till vitt ( i bemärkelsen konstant fördelning). Här ett exempel i gult och blått.
4. Här har du gult och blått (eller blåviolett) som idealiserade spektralfördelningar.
5. Magenta och grönt i form av idealiserade fördelningar.
6. Här kan komplementfärger konstrueras efter eget val. Till vänster har du vitt (dvs ett full-spektrum) till höger så gott som svart. Nu för du över mer och mer från det vita till mörkret och där växer fram en färg som är komplementär till den färg som samtidigt uppstår på den vänstra sidan, vartefter som du modifierar fullspektrum. Lägg märke till att komplementfärger kan vara såväl starka kulörer som färgsvaga, pastellartade. Ja, kan i gränsfallet t.o.m. vara två stycken grå.
Upprepade tryck på 6 ger dig möjlighet att utgå från annan nivå i diagrammen.
Genom tryck på 9 kan du beställa fram ett par fördelningar du tidigare tillverkat i tablå 2.
TABLÅ 4: Belysning på metamera färgprover
Här ökas komplikationsgraden, i och med att vi har tre spektralfördelningar inblandade. I praktiken är det nämligen vanligtvis så, att metamera ljusflöden uppstår genom att två färgmaterial - filter eller färgytor - med olika spektral transmittans resp reflektans, betraktas i belysning av ljus med en viss spektralfördelning, i vilken de två materialen ser lika ut. De säges då vara metamera under denna belysning. I annan belysning (dvs belysning med annan spektral energifördelning) kan de skilja sig åt i färg. Så här ser tablån ut:
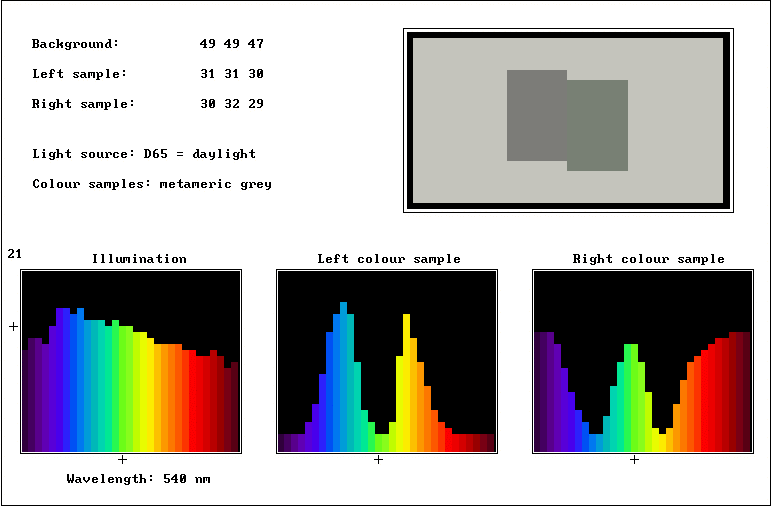
I första rutan kan man (med tangenterna 1 t.o.m. 4) välja endera av fyra ljuskällor. Med tangenterna 5 t.o.m. 8 kan väljas diverse exempel på metamera färgmaterial, som visas i rutorna left colour sample och right colour sample.
De belysningar du kan välja mellan är:
Belysningen kan modifieras med piltangenterna och sparas med S samt senare återhämtas med tangent 0.
De färdiga exemplen (tangent 5-8) är:
För vart och ett av dem: studera dem i de olika belysningarna 1 - 4 !
Du kan tillverka egna exempel i tablå 2 och ta in dem här genom tryck på 9 !
TABLÅ 5: Illustration av subtraktiv färgblandning
Ett annat exempel på en situation, där tre spektralfördelningar är inblandade, är s.k. subtraktiv färgblandning. Ett ljusflöde passerar genom två färgfilter och modifieras successivt. Exempelvis först ett gult, därefter ett ljusblått, med samma resultat som om det passerat ett grönt filter. Tablån förklarar varför det blir så. Och varför det, i vissa fall, kan bli så att två filter, lagda på varandra, ger "svart", dvs ett ogenomskinligt filter; liksom att flera filter av ett och samma slag, lagda på varandra, kan ge en annan färg. Exempelvis två gröna filter, som lagda på varandra blir ett rött filter (s.k. dikroism).
De färdiga exemplen är följande:
På sedvanligt vis kan du välja ett av exemplen som utgångspunkt (t.ex. nr 4!) och modifiera de två fördelningarna med hjälp av piltangenterna (och växla med mellanslags-tangenten). Du kan spara ett eget par av fördelningar med S (och hämta tillbaks det med 0). Du kan tillverka ett par i tablå 2 och hämta hit det med 9. Undersök exempelvis hur metamera fördelningar beter sig vid successiv verkan! Hur går det med komplementära fördelningar?
Anmärkning: Tablån kan även tolkas som att ett färgat ljus (spektralfördelning 1) belyser ett färgmaterial (fördelning 2) med fördelning 3 som resultat - och hur denna ser ut visas i lilla rutan upptill.
Ytterligare övningar
De grundläggande undersökningarna av färgseendet utfördes i allmänhet med spektralrent ljus, dvs ljus med med smalt avgränsat våglängdsområde, exempelvis ljus från urladdningslampor. Du kan pröva på att blanda färger med hjälp av tre spektralkomponenter. Välj för det ändamålet tablå 2.
Med 620 nm, 540 nm och 460 nm täcker du gott och väl in alla färger som går att få fram i datorskärmens RGB-system. Sätt upp nr 5 (grönt) i vänstra diagrammet. Tryck X. Gå därefter till högra diagrammet. Tryck 8 och använd bakgrundsnivå noll. Dra upp lite av vardera av de tre våglängderna. Tryck X. Justera tills du får match med den gröna. Pröva på samma vis att matcha några andra färger. Pröva gärna även att utgå från andra kombinationer av våglängder. Exempelvis kan man i ena diagrammet sätta upp 610, 550, 470 och i det andra 620,540, 460 och jämföra hur de ser ut, exempelvis när båda ger vitt (dvs 63 63 63).
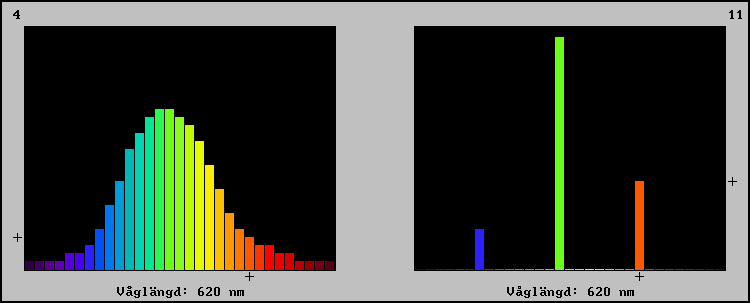
Slutligen kan du övertyga dig om att grått, dvs en neutral, konstant fördelning (nr 4 i tablå 2) även kan matchas mot en blandning av endast två spektrallinjer, förutsatt att de valts vid rätt våglängder. Pröva 580 nm tillsammans med 480 nm! Undersök om du hittar ett annat användbart par.
Komplementfärger kan som du märkt betyda en hel del olika saker ur fysikalisk synpunkt. Det kan vara färgerna hos två spektralfördelningar som adderade ger en konstant fördelning. Sådana fördelningar kan mycket väl ha våglängder gemen-samt, dvs de ger inte svart vid subtraktiv blandning. Strikt komplementaritet får man om man dessutom ställer kravet på att de båda fördelningarna inte får ha någon våglängd gemensam. Som filter, lagda på varandra, släpper de då inte igenom något ljus. Strikt komplementaritet kan idealiserade fördelningar ha - som de i tablå 3, nr 4 och 5. (De ger visserligen inte svart utan mörkgrått vid subtraktiv blandning, på grund av att de har en liten neutral bakgrund för att kunna återges på skärmen., men i vart fall inte grönt, som man skulle vänta sig att gult och blått gör.)
Om man har ett par "äkta" komplementära fördelningar, kan man få samma färger som de har genom att välja godtyckliga andra fördelningar ur de ekvivalens-klasser som respektive fördelning tillhör. Det är så det faktum, att till och med enstaka våglängder parvis kan vara komplementfärger, förklaras.
Några viktiga frågor
1) Hur pass trovärdig är den färg som visas i rutan på bildskärmen? Det är en knivig fråga, ty vilken färg som ljus med given spektralfördelning i en situation kommer att motsvara beror på sammanhanget. Sambandet mellan spektralfördelning och färg är inte fixerat utan variabelt. Vad programmet gör, är att, i den lilla rutan på skärmen, presentera ett ljus som för en standardobservatör är ekvivalent med det ljus som skulle ha den spektrala energifördelning som diagrammet visar. Ekvivalensen innebär att de två ljusflödena, under i övrigt identiskt lika förhållanden, skulle ge upphov till exakt samma färgintryck, - men vilken färg, det beror på sammanhanget, dvs omgivande fält m.m. I vårt fall är den visuella situationen den, att man ser en liten ruta mot grå bakgrund, på vilken också finns en del text i vitt och ett färgrikt diagram. Bildskärmar har vanligtvis ett kyligt vitt ljus; snarare dagsljusliknande än glödlampsljusliknande. Det tänker man inte på, om man huvudsakligen tittar på skärmen, men om man direkt jämför ett vit pappersark, belyst av glödlampsljus eller av ljuset i ett solupplyst rum, då märker man skärmens blåaktigt vita ton. Under lite mer normala belysningsförhållanden, skulle den aktuella spektralfördelningen, som visas i lilla rutan på skärmen, motsvara en något kyligare kulör, än den som syns på bildskärmen.
Not. Om du trycker tangent X så får du se en färg som kompenserats för skärmens kylighet, så att konstant fördelning motsvarar rent grått (och inte lite brunaktigt grått). Pedagogiskt kan det vara en lämpligare variant, även om den icke exakt visar ekvivalent spetralfördelning.
2) Hur kalibrerar man programmet mot bildskärmen? Ytterligare en förutsättning för att den färg som visas skall vara trovärdig, är att programmet är kalibrerat mot bildskärmen. Bildskärmen är inställd på en eller annan vitpunkt - dvs. förhållande mellan ljusstyrkan hos den röda, den gröna och den blå fosforen, vid maximal utstyrning av alla tre. Vitpunkten anges vanligen med "färgtemperatur" (color temperature), egentligen "korrelerad färgtemperatur". På nyare skärmar kan vitpunkten ställas in. Välj i så fall 7000 K eller 6500 K. (Äldre skärmar har mycket blåaktig vitpunkt, 9300 K) Kalibreringen sitter i datafilen "matris.d" som anger den 3x3-matris som ombesörjer den linjära transformationen mellan CIE kolorimetriska koordinater X,Y,Z till (r,g,b) dvs utstyrningen av de tre fosforerna R, G och B.
3) Finn det färger som ligger utanför RGB-triangeln? Vissa spektralfördelningar motsvarar ett ljus som inte går att matcha mot någon kombination av R, G och B. Det betyder, att de motsvarar färger som inte går att få fram på bildskärmen. Det gäller färgstarka, mättade kulörer - i synnerhet i rent grönt eller turkos, men faktiskt även i gult, rött och purpur. Den typen av ljus får man t.ex. med lysdioder och laser, men knappast med sedvanliga pigmenterade ytor, belysta med dagsljus eller glödlampsljus. Däremot kan man, med transparenta färgfilter, tillsammans med glödlampsljus, få fram ljus med intensivare färg, än vad som går att få fram på en elektronisk bildskärm. Eftersom programmet avses vara "korrekt", så visas den motsvarande färgen (eller ekvivalenta RGB-kombinationen) bara för de spektra som kan återges korrekt.
4) Kan verkligen ett rent spektrum visas på skärmen? Undantaget från denna princip är det kolorerade spektrum, som gör diagrammet trevligt att titta på. Det är endast en illustration - våglängdsrent (monoenergetiskt) ljus går inte att återge på bildskärm. Ambitionen har dock varit att, vad gäller kulörtonen, någotsånär riktigt återge utseendet av ett linjärt spektrum, alltså ett gitterspektrum. Erfarenhetsmässigt ligger den rent gula våglängden (ett gult som varken är rödaktigt eller grönaktigt gult) vid 580 nm och är ett förhållandevis smalt område, jämfört med de våglängder som ser huvudsakligen röda, resp. gröna ut. Redan vid 600 nm har man en orange kulör, som är lika gulaktig som rödaktig. På samma sätt ligger vid 500 nm en turkos färg, som är lika grönaktig som blåaktig. Den rent blå ligger (lite mer diffust lokaliserad) kring 470 nm. Hela intervallet från 510 nm till 570 nm gör väsentligen ett grönt intryck. Ljusheten i spektrum är störst vid 550 nm och avtar därifrån tämligen symmetriskt ut mot korta och långa våglängder. Om du vill, kan du justera färgerna i det spektrum som pryder programmets diagram. De anges i datafilerna high.d och low.d som taltripplar r g b, vilka kan anta värden mellan noll och 63. (Orsaken till att de trettio kulörerna är uppdelade på två datafiler är att man lämpligtvis kan trimma in dem mot varandra i tablån "färgskalor" i datorprogrammet "Färglära på datorn" och därifrån direkt spara dem som ASCII-filer som kan läsas in av det här programmet.)
5) Varför energi mot våglängd i diagrammet? Eftersom detekteringen i tapparna i retina är en fotokemisk process så vore det mest adekvat att ange fotontätheten i ljusflödet mot fotonenergin (dvs frekvensen). I så fall blir en konstantfunktion tämligen nära motsvarande vad man upplever som neutralt, vitt ljus, dvs en färgtemperatur av omkring 6500 K. På grund av att vad man i första hand mäter är våglängd och intensitet (=energi) hos ljusstrålningen så har det dock etablerats en praxis att man i diagrammen visar spektral energifördelning mot våglängd. Jag har inte funnit tillräcklig anledning att frångå denna praxis i det här, väsentligen praktiskt pedagogiska programmet.
(spektra.doc 99-10-08)