Experiment med färgade ljusflöden

Första undersökningen

Additiv färgblandning demonstreras kanske allra mes åskådligt med färgade ljusflöden. Vi tänker oss att vi befinner oss i ett mörkt rum. Tre diabildsprojektorer är uppställda, var och en försedd med en "diabild" som helt enkelt är en fyrkantig kartongbit 5x5 cm med ett utskuret runt hål i. På en vit skärm eller vägg projiceras de tre bilderna: det blir tre runda ljusfläckar. Framför objektiven kan färgfolier placera, så att rundlarna får olika färger.

Typfallet är att man har en röd, en grön och en blå färgfolie, så att vad man ser är detta:

Vi riktar nu projektorn med det röda filtret så att den röda ljuskäglan delvis sammanfaller med den gröna:

Det uppstår gult, som i den bemärkelsen kan sägas vara en blandning av rött och grönt, eller noggrannare beskrivet orangerött och gulgrönt, eller hur! Och inte heller rätt och slätt bara en "blandning", utan en ren addition. Ty fysikaliskt gäller, för två ljusflöden som förs samman, att de inte "märker av" varandra, inte påverkar varandra, utan just bara "adderas".

Nästa steg i demonstrationen är att den blå ljuskäglan riktas så att den kommer att delvis överlappa de andra två:

Där det blå adderas till det röda uppstår en blåröd färg, kallad magenta. Där det adderas till grönt uppstår en blågrön, turkos kkulör, kallad cyan och där alla tre ljusflödena sammanfaller får vi vitt. Detta under förutsättning att ljusintensiteterna hos de tre ljusflödena är inställda så att de på detta sätt balanserar varandra.

Detta, att färgade ljusflöden i addition kan "balansera" varandra, dvs att kulörer kan neutralisera varandra, som vore det motriktade krafter, var något som Newton i sina undersökningar för trehundra år sedan tog fasta på, när han lade grunden till den fysikaliska teorin för färg, kolorimetrin. Spektrums kulörer bör rätteligen representeras på en del av en cirkel, vars centrum är just neutralpunkten, "vitt" (eg. hela skalan av akromatiska färger mellan vitt och svart).

Men det leder oss också till det viktiga begreppet KOMPLEMENTARITET. För när det blå adderas till det gula fältet uppstår ju vitt, dvs gulheten och blåheten tycks helt upphäva varandra - de två ljusflöden s.a.s. kompletterar varandra till vitt.

Å andra sidan kan man uttrycka det som att gult ljus är vitt ljus minus blått. Det gula filtrets verkan är att absorbera den blå komponenten i ljuset från projektorlampan. Vi kan schematisk summera sakförhållandet så här:

Om Y=R+G och R+G+B=W så kan vi också säga att Y=W-B

På samma sätt kan vi i vår demonstration peka på två andra komplementära färger. Vardera av "sekundärfärgerna" är komplementär till den tredje "primärfärgen":

Vi kan notera detta sakförhållande så här Y+B = M+G = C+R = W

Ett vackert exempel på additiva komplementfärger ges av de färger som uppträder i samband med POLARISERAT LJUS.

Andra undersökningen

Nu skall vi blanda färgade skuggor i stället för färgade belysningar. Låt därför ljusflödena från de tre strålkastarna, försedda med rött, grönt och blått filter, bli så vida, att de alla tre helt lyser upp den vita skärmen. Den synes då vit helt enkelt. Placera nu framför skärmen ett ogenomskinligt föremål, som kastar tre färgade skuggor på den vita ytan.

Placeras föremålet tillräckligt nära skärmen kommer skuggorna att överlappa och då bildas blandfärger, som synes. Där alla tre skuggorna överlappar blir det svart.

Hur skall detta förklaras? Jo, med hjälp av skuggkastaren subtraherar man en del av ljuset som belyser skärmen. Där ljuset från den röda strålkastaren skyms blir det en turkos skugga. Där ljuset från den blå strålkastaren skyms blir det en gul skugga. Förs dessa båda skuggor ihop, innebär det att både den röda och den blå strålkastaren undanskyms, kvar blir bara belysningen från den gröna. Alltså blir blandfärgen grön o.s.v.

Vi konstaterar: Skuggor blandas subtraktivt, liksom dagrar blandas additivt.

Tredje undersökningen

Så långt de grundläggande demonstrationerna av principen för "additiv och subtraktiv färgblandning", med hjälp av strålkastare med färgat ljus. Nu skall vi göra vissa iakttagelser, som innebär en problematisering av den enkla teorin, men som är viktiga för förståelsen av färgseendets gestaltande kraft.

När Goethe, i sin färglära - och i uttrycklig polemik mot Newtons idéer om färg - tar upp begreppet färgblandning, gör han det med följande skeptiska kommentar:

Varje blandning förutsätter i princip en specifikation och vi befinner oss därför, så snart vi talar om blandning, på det atomistiska fältet. Man måste först tänka sig visa kroppar specificerade till den ena och andra punkten på färgkretsen, innan man kan tala om att genom blandning av dem frambringa nya schatteringar.

Vad menade han månntro med detta? Låt oss börja om från början igen och gå igenom demonstrationen av hur nya färger uppstår när avgränsade ljusflöden adderas, och denna gång vara mer noggranna och uppmärksamma på vad som verkligen sker.

Låt oss alltså återigen åtskilja ljuskäglorna från de tre projektorerna och till att börja med ta bort färgfiltren. Alltså har vi tre runda ljusfläckar - i det ideala fallet är de alla tre precis lika:

Nu riktar vi den vänstra projektorn så att dess ljusflöde delvis faller på den mittre rundeln.

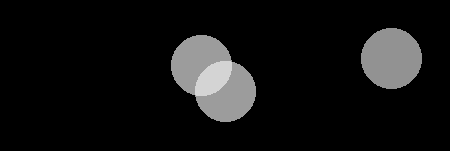
Vad händer? Jo det uppstår vitt där de två överlappar. Helt naturligt, eftersom belysningsstyrkan där är dubbelt så stor som på de ställen där bara en projektor lyser. (I enlighet med den fysikaliska principen att ljusflöden blott och bart adderas.)

Men lägg märke till att vad som också händer, är att de angränsande fälten tydligt framstår som grå. De får liksom sin gråhet tillföljd av relationen till det vita.

Låt oss nu tillfoga även den tredje projektorns ljusflöde. Då ter det sig så här:

Vad har hänt? Jo, det fält som nyss var vitt, är inte längre vitt. Det har nu blivit ljusgrått. I stället är det där alla tre ljusflödena sammanfaller som vi ser vitt.

Genom att partiellt sammanföra fler och fler belysningar kan man bygga upp en gråskala. Grunderfarenheten är: Det starkast belysta fältet får rollen av vitt och övriga fält får mer eller mindre gråhet.

Så vad vi antar fysikaliskt oförändrat är inte visuellt oförändrat. Tillför vi ett nytt ljus så ändras färgen inte bara där det ljuset träffar utan även på angränsande fält! Den strikt fysikaliska beskrivningen skiljer sig från den fenomenologiska, dvs den som handlar om vad vi faktiskt ser.

Låt oss gå vidare och laborera med färgade ljusflöden. Vi börjar med två projektorer, släcker för tillfället den tredje. Framför den ena av dem placeras en blå folie. Då ser vi följande:

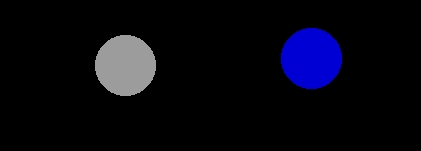
Så sammanför vi de två, så att de kraftigt överlappar, ja, nästan helt sammanfaller ett ögonblick, sedan kan vi dra isär dem lite. Och, se! När den förut "vita" rundeln - alltså den som är rent ofärgat projektorljus - tittar fram är den tydligt gul.

(Detta är i det verkliga försöket mer påfallande än här på skärmen. Men kika på figuren nedan genom ett papprör så att du inte störs av omgivningen! Har du en LCD-skärm, exvis laptop, kan du röra på huvudet och betrakta skärmen snett nedifrån - hur bilden ser ut är starkt beroende av betraktningsvinkeln, för den typen av bildskärmar.)

Att det kommer gulhet över det förut grå fältet har att göra med vad jag nyss nämnde, nämligen att den ljusaste ytan i synfältet alltid tenderar mot att uppfattas som vit. Så det ljusblå fältet förlorar i samma mån i blåhet.

Nu kan vi gå vidare till försök med alla tre projektorerna. Vi börjar med att ha den ena släckt och placerar ett rött respektive ett blått filter framför de andra två, som får lysa så att de lysande rundlarna delvis överlappar:

Så tänder vi den tredje projektorn, vars ljusflöde alltså inte färgats med hjälp av någon färgfolie.

Om du tittar på den här figuren en stund så blir det alltmer tydligt hur det undre fältet drar iväg mot grönt. Ett ganska färgsvagt grönt,visserligen, men i vart fall åt det gröna hållet. Och överlappningen med rött ser ganska rent gul ut. Liksom det rosa mittfältet förskjuts mot vitt. Ögat möblerar liksom om figuren, gestaltar bilden till en balanserad helhet. Resultatet närmar sig den traditionella ikonen för "additiv färgblandning". Det är som om vårt synsinne vill ha det så.

Det innebär - och det var förstås detta Goethe antydde med det ovan citerade uttalandet - att det är fundamental skillnad mellan vår sinnesåskådning och den fysikaliska beskrivningen av världen. Den senare driver i möjligaste mån tesen om världen som sammansatt av beståndsdelar vilka bibehåller sina egenskaper ofröändrade när de sammanfogas. Sinnesåskådningen, framför allt den visuella bilden av världen, som ju bygger på framställandet av omvärlden som ett "bredvid-vartannat", lyckas trots allt inte driva den tesen fullt ut. Verkligheten motsätter sig inför sinnena att låta sig helt och fullt fragmenteras.

Praktiskt, pedagogiskt, betyder det, att det inte är en helt lyckad demonstration av additiv färgblandning att projicera tre bara delvis överlappande färgade ljusrundlar. Ty den figur som bildas har en tendens att se ut just så, som den gör, till viss grad oberoende av det fysikaliska tillståndet hos de tre ljusen vi adderar. Ur visuell synpunkt fungerar "blandningen" i detta försök inte additivt. Enda sättet att undvika detta gestaltpsykologiska problem, när man vill demonstrera principen för additiv färgblandningen, är genom att låta de tre ljusrundlarna helt och precist sammanfalla, så att de bildar en enda rundel, vilken då antar den additiva blandfärgen. Detta är svårt att åstadkomma utan komplicerad apparatur. Enklast bekantar man sig därför med additiv färgblandning med hjälp av en elektronisk bildskärm. (Se den tredje tablån i mitt pedagogiska datorprogram "RGB"!)

Kommentar, tillfogad 2003-11-09:

Det finns ytterligare skäl till att det traditionell accepterade ideogrammet (med tre delvis överlappande cirklar) är tvivelaktigt för åskådliggörande av additiv färgblandning. Saken blir ännu tydligare, om man ger det formen av tre delvis överlappande kvadrater. Det ser då ut som tre genomskinliga färgade plattor som delvis ligger på varandra, dvs framskymtar genom varandra. Ännu mer oemotståndlig blir illusionen om man gör de tre fyrkanterna rörliga, så att de kan dras isär, respektive föras ihop, så man ser hur blandfärgerna uppstår i det ögonblick plattorna möts, dvs delvis upptar samma position i synriktningen. Vi uppfattar alltså spontant bilden här nedan som tre kvadratiska plattor, inte som sju plattor, med diverse former. Tänker jag mig exempelvis att jag drar undan det blå fältet, föreställer jag mig att även magenta, turkos och vitt försvinner. Men egentligen, på skärmen, är det sju skilda fält, vart och ett med sin färg. Tar jag bort blått försvinner bara det och inget mer!

Föreställer man sig det som tre kvadratiska plattor, då illustrerar figuren snarare subtraktiv blandning (t.ex. tre färgfilter lagda på varandra). Men i så fall borde inte gult bildas av rött och grönt; gult kan inte vara "rött sett genom grönt" eller "grönt, sett genom rött". Problemet är att det för våra ögon ter sig som homogent färgade fält. (Beroende på att färgpunkterna, som bygger upp bilden, är så små. Det gula fältet är noga besett bara röda och gröna prickar.) Detta är grundläggande i det sätt på vilket vårt öga (synsinne) gestaltar synintrycket. Det bildas tre självständiga gestalter - bilden tycks oss åskådliggöra ting i ett rumsligt förhållande till varandra. Ett förhållande av "framför/bakom". Fast det "egentligen" bara är bildskärmens plana yta, där allt måste vara "bredvid-vartannat".

Därför bord det vara ett mer rättvisande sätt att åskådliggöra additiv blandning genom zoomning: Visa ett tydligt raster uppbyggt av de tre färgerna R, G och B och successivt förminska det tills de flyter samman till en enhetlig färg.

Jo, men är det alltså inte trots allt bäst att demonstrera additiv blandning med flöden från tre verkliga strålkastare, alltså som en process i rummet? Så vill ju eleverna helst ha det - på datorn kan man ju fejka allting, säger de. Det sista är långt ifrån helt sant - men, OK, det har sin poäng att visa blandning av färgade ljusflöden med hjälp av tre strålkastare eller tre diaprojektorer. Men även i det fallet finns finns en hake: Hur kommer det sig, hur är det överhuvudtaget möjligt, begripligt, att de tre ljusflödena kan träffa samma ställe på den belysta ytan utan att kollidera, utan att påverka varandra - hur kan de befinna sig på samma plats i rummet utan att trängas, utan att undanskymma varandra? Det var en gåta naturfilosofer i långliga tider grubblat på. Fysikerna gav den ett namn: superpositionsprincipen.

Men att man hittar på ett namn på en gåta är inget svar, fast det kan kännas så för den som läser in en kurs i optik. Tänk efter: Om det är så att ljus kan befinna sig på en och samma plats utan trängsel kan det inte vara något materiellt. Alltså: ljuset är immateriellt. Nåväl, det är inget mystiskt med det. Vi känner till andra immateriella företeelser, t.ex. en våg som rör sig fram över en vattenyta. Eller ett ljud i luften. Vågen tar tillfälligt form i vattenmaterien där den drar fram - vattnet är dess substans, dess materiella bärare, men den byter fortlöpande materia vartefter som den fortskrider. Och med (ideala) vågor är det faktiskt så att de kan mötas, korsa varandra på ett och samma ställe, utan att inverka på varandra - de bara adderas. Alltså: ljuset är måhända en vågrörelse - men vad är i så fall det bärande mediet, motsvarande luften, vattnet?

En annan möjlighet är att ljuset inte är homogent - att det, i likhet med materiella kroppar, till största delen består av tomrum. Att ljusflödet från en strålkastare är en gles ström av partiklar, där det i mikrokosmos (om vi upplöser tid och rum tillräckligt fint) är långt mellan partiklarna, så att risken för kollison eller "trängsel" är nära nog obefintlig. Samt att det är långt i tiden, mellan absorptionshändelserna, dvs händelsen, att en ljuspartikel träffar en molekyl på den belysta ytan. Så ibland är det en ljuspartikel från den röda strålkastaren, ibland från den gröna, ibland från den blå. Men aldrig märker de av varandra.

ÅTER TILL HUVUDTEXTEN OM FÄRGBLANDNING